赤道座標と銀河座標は、どちらも、主に地球から観測した恒星や銀河の位置を表すのに使われます。天体についてのデータベースや星図を作ったりする際に、これらの座標の変換を行うことがあります。
この記事では、高等学校程度の数学とプログラミングの知識で、赤道座標と銀河座標の間の座標変換を行う方法を解説します。
赤道座標と銀河座標の間の座標変換については、この Wikipediaの 記事 にあるように、既に公式が知られています。そのため、公式を使った計算さえできればよい、というのであれば、この記事を読む必要はありません。
その一方、この記事では、赤道座標と銀河座標の幾何学的な関係から、座標に対してどのような計算を行えばよいのかを考える手順について解説します。これは、赤道座標と銀河座標だけに限らず、他の球面座標間での座標変換にも応用できます。
三角関数の計算は面倒だったりしますが、手順を理解して丁寧に計算をすれば、自分で座標変換の公式を導き出すこともできると思います。しかし、そのような計算は大学のレポート課題くらいでしか行うことはないでしょう。現実的には、コンピューターを使って数値的に座標変換を行うことの方が多いと思います。
そこで、この記事ではアルゴリズムを示すために、所々に C# によるサンプルコードを載せています。ただし、読みやすさを重視するために、それらのコードは必ずしも効率や精度の良いものとはなっていません。また、サンプルコードは単体では動作しないので、クラスの内部に含めるなど、書き換えが必要になります。あくまで自分でコードを書く際の参考としてください。
ここでは、サンプルコードを理解するために必要な C# の特徴を挙げておきます。
まず、C# では変数を宣言する際、型を指定しなければなりません。例えば、
int i = 0;
double x = 1.0;
というように、整数は int、倍精度浮動小数点数は double、などと宣言しなければなりません。
こうして宣言された変数は、double 型のような数値であっても オブジェクト で、関数を呼び出す際に、値を渡すことも、参照を渡すこともできます。
関数への参照渡しを使えば、1つの関数から複数の計算結果を取り出すことができます。次の例を見てください。
private void sample()
{
double x = 1.0;
double y = 2.0;
double a = 3.0;
double b = 4.0;
function(ref x, ref y, a, b);
// ここでの値は次の通り。
// x = 5.0、y = 22.0、a = 3.0、b = 4.0。
// x と y は変化するが、a と b は変化しない。
}
private void function(ref double x, ref double y, double a, double b)
{
x = a * x + y; // x の値は 5.0。
y = b * x + y; // y の値は 22.0。
a = a + b; // a の値は 7.0。
b = x + y; // b の値は 27.0。
}
C# では、変数の参照を関数に渡す場合、引数の前に ref を書きます。この例では sample から function を呼び出すときに、x と y の参照が渡され、a と b の値が渡されています。
function の中で色々と計算をした結果、function の終わりの部分で、x、y、a、b、の値は変化しています。しかし、a、b、については値のコピーを function に渡しているので、sample の側では値が変化しません。
これに対し、x、y、については、変数を操作することのできる参照を function に渡しているので、sample の側でも値が変化します。
つまり、2つの計算結果 x と y を function から sample の側に取り出すことができるのです。
角度の変換
私たちの日常の生活では通常、直角を 90°、一周を 360° とする 度数法 で角度を表記します。しかし、赤道座標では、赤緯は度数法で表記するものの、赤経については、直角を 6h、一周を 24h とする 時間表記 を用います。
これらの度数法と時間表記では、より小さな 60進法による単位が
1° = 60′ = 3600″
1h = 60m = 3600s
と定められています。それぞれの単位は、度数法が、度、分、秒、時間表記が、時、分、秒、となっています。
一方、プログラミング言語で三角関数を呼び出す際は、直角を \(\pi\)/2、一周を 2\(\pi\) とする 弧度法 がよく用いられます。ここで \(\pi\) は 円周率 を表します。
弧度法によって角度を表記した場合の単位は rad(ラジアン)で、\(\pi\)/2 rad などと表記するのですが、特に誤解される恐れがなければ、この rad は省略されることが多いです。
コンピューターで三角関数を使った計算を行う場合は、度数法や時間表記による角度を弧度法に変換し、計算を終えた後で、再び、度数法や時間表記に戻す、という作業が必要になります。
まず、度、分、秒、のように3つの変数で表されている角度を、1つの変数にまとめましょう。
private double dmsToDegree(double d, double m, double s)
{
return d + m / 60.0 + s / 3600.0;
}
この関数を使うと、度数法でも時間表記でも、分や秒の部分を小数値に変換した度や時の値を計算できます。
ここでひとつ注意があります。
天体についてのデータベースなどでは、例えば、恒星の位置などが、
|ra |dec
|14 26 55.7408|-83 40 04.271
|22 46 03.7233|-81 22 53.822
といった形式で書かれていたりします。この ra は赤経で時間表記であり、dec は赤緯で度数法による表記です。このように書かれた赤緯や銀緯は、うっかりすると計算を間違えます。
1行目について見ると、赤緯は、マイナス83度40分04.271秒です。これを
double d = -83.0;
double m = 40.0;
double s = 4.271;
double degree = dmsToDegree(d, m, s);
とやってしまいがちなのです。負の角度の場合、正しくは、
double d = -83.0;
double m = -40.0;
double s = -4.271;
double degree = dmsToDegree(d, m, s);
としなければなりません。
分と秒を少数にして角度の変数を1つにまとめたので、これをラジアンに変換します。
private double degreeToRadian(double degree)
{
return degree / 180.0 * Math.PI;
}
private double hourToRadian(double hour)
{
return hour / 12.0 * Math.PI;
}
Math.PI は円周率です。半周が 180° = 12h = \(\pi\) rad であることを使っています。プログラミング言語や処理系によっては、度数法による角度をラジアンに変換するメソッドがライブラリで用意されている場合があります。
ラジアンから度や時に変換するには、
private double radianToDegree(double radian)
{
return radian / Math.PI * 180.0;
}
private double radianToHour(double radian)
{
return radian / Math.PI * 12.0;
}
などとすればよいでしょう。
これを更に、度、分、秒、のように3つの変数に分けるには、変数を整数部と小数部に分ける、といった作業が必要です。プログラミング言語や処理系によって、いろいろな方法があり得るので、自分の環境に合わせて考えてみてください。
2次元の回転
球面座標間の座標変換では、3次元の回転を扱う必要があります。まず、いきなり3次元について考える前に、2次元の回転について考えておきます。
平面上に直交座標系 \(E\) が設置されているとします。
この平面上にある図形 \(S\) を、原点を中心に反時計回りに角 \(\theta\) だけ回転させる操作を \(\hat{R}(\theta)\) とします。回転後の図形を \(S^\prime\) とすると、
\(S^\prime = \hat{R}(\theta)\,S\)
と書くことができます。
特に、図形 \(S\) が1つの点 \(P\) の場合、\(P\) は回転 \(\hat{R}(\theta)\) によって \(P^\prime\) に移動します。
\(P^\prime = \hat{R}(\theta)\,P\)
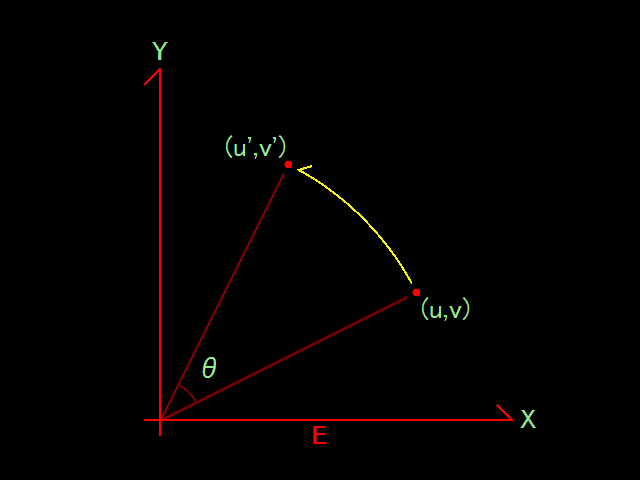
このとき、\(P\) の座標を \((u,v)\) とすると、回転後の \(P^\prime\) の座標 \((u^\prime,v^\prime)\) は
\( \left\{ \begin{array}{l} u^\prime = u \cos\theta \,\, – \,\, v \sin\theta \\ v^\prime = u \sin\theta \, + \, v \cos\theta \\ \end{array} \right. \)
で計算することができます。これを、次のように書き換えておきます。
\( \left( \begin{array}{c} u^\prime \\ v^\prime \\ \end{array} \right) = M(\theta) \left( \begin{array}{c} u \\ v \\ \end{array} \right) \)
このような形にすると、計算の操作 \(M(\theta)\) と、計算を施す対象 \((u,v)\) を分けることができます。
この表記が分かりにくければ、とりあえず、右辺の \(\theta\)、\(u\)、\(v\) を使って、左辺の \(u^\prime\)、\(v^\prime\) が計算される、と思ってください。
2次元空間で点を回転させる場合の回転後の座標は、次のようなコードで計算することができます。
private void rotate(ref double u, ref double v, double radian)
{
double w = u * Math.Cos(radian) - v * Math.Sin(radian);
v = u * Math.Sin(radian) + v * Math.Cos(radian);
u = w;
}
参照を使って、回転後の u と v の計算結果を関数外に取り出すことに注意してください。
私は最初に高等学校で行列を学んだのですが、現在は、高等学校で行列を教えていないようです。そこで、回転を表す行列について触れておきます。
座標 \((u,v)\) にある点を角 \(\theta\) 回転させるとき、回転後の座標は行列を使った式
\( \left( \begin{array}{c} u^\prime \\ v^\prime \\ \end{array} \right) = \left( \begin{array}{cc} \cos\theta & -\sin\theta \\ \sin\theta & \cos\theta \\ \end{array} \right) \left( \begin{array}{c} u \\ v \\ \end{array} \right) \)
で計算することができます。つまり、\(M(\theta)\) の正体はこの行列です。
2次元の場合、行列と座標やベクトルの積は、
\( \left( \begin{array}{cc} a & b \\ c & d \\ \end{array} \right) \left( \begin{array}{c} u \\ v \\ \end{array} \right) = \left( \begin{array}{c} au + bv \\ cu + dv \\ \end{array} \right) \)
と計算されます。これを使って点の回転について、行列を使う場合と使わない場合の式を比べてみてください。
回転を表す行列は、いろいろと使い道があるので、公式として覚えておくとよいでしょう。
私は高校生の時に、回転行列を
\( \left( \begin{array}{cc} \cos\theta & -\sin\theta \\ \sin\theta & \cos\theta \\ \end{array} \right) \Rightarrow \left( \begin{array}{cc} \mbox{こすい} & \mbox{婆さん} \\ \mbox{死んでも} & \mbox{こすい} \\ \end{array} \right) \)
などと教わったものです。今こんなことを教えたら、きっと怒られるでしょうね。
座標やベクトルの変換を行列を使って表すと、行列の固有値、固有ベクトルや、行列式を計算することで、変換の性質について知ることができるようになります。詳しく知りたければ、線形代数を学んでください。
ここで、図形 \(S\) として直交座標系 \(E\) の座標軸をとり、これを角 \(\theta\) 回転させます。そして、回転後の座標軸を使って、新たな直交座標系 \(G\) を設置します。
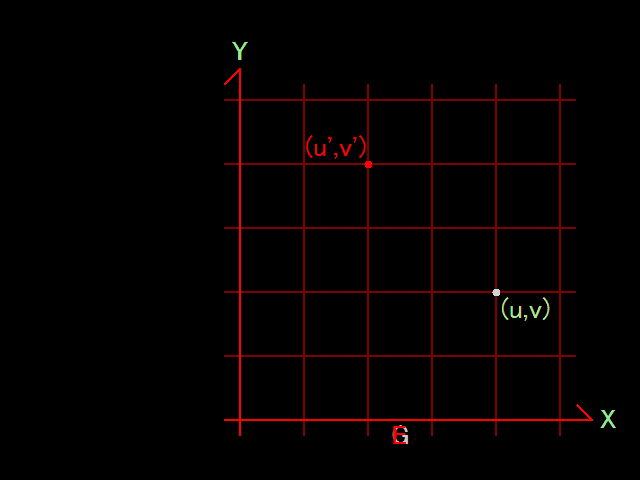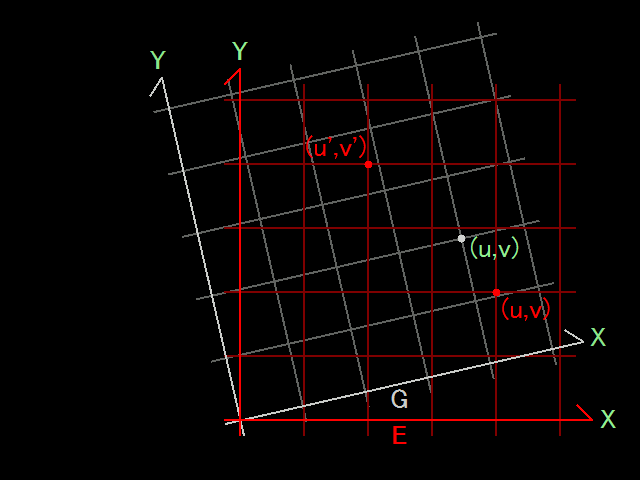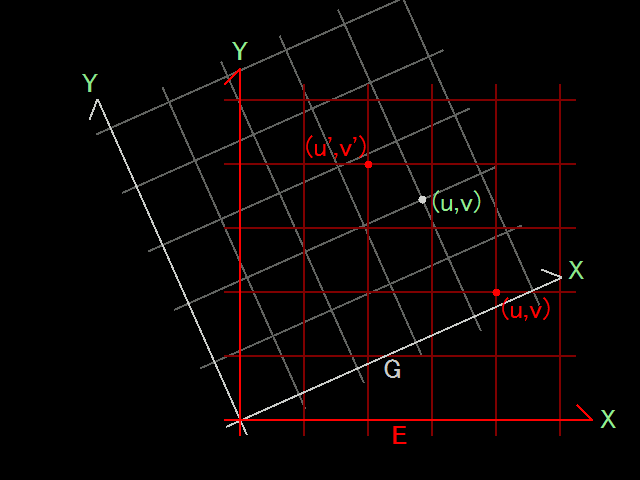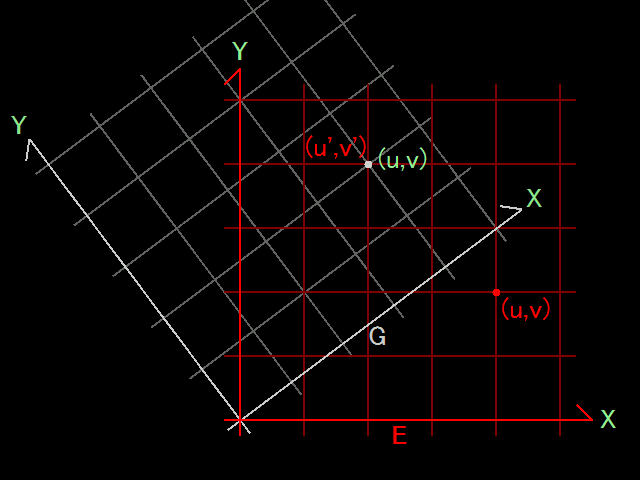
\(S\) と一緒に、先程の点 \(P\) を回転させたとします。すると、\(S\) と \(P\) の位置関係は、回転の前後で変化しません。そのため、座標系 \(G\) でのこの点の座標は \((u,v)\) のままです。
その一方、座標系 \(E\) から見ると、この点は角 \(\theta\) の回転をして、その座標が \((u^\prime,v^\prime)\) に変化します。
これらのことから、座標系 \(G\) での座標を座標系 \(E\) での座標に変換する式は、
\( \left( \begin{array}{c} u^\prime \\ v^\prime \\ \end{array} \right) = M(\theta) \left( \begin{array}{c} u \\ v \\ \end{array} \right) \)
である、と分かります。
この式の逆変換、つまり、座標系 \(E\) での座標を座標系 \(G\) での座標に変換する式について考えます。上の \(G\) から \(E\) への変換式の両辺に \(M(-\theta)\) の計算を施すと、
\( M(-\theta) \left( \begin{array}{c} u^\prime \\ v^\prime \\ \end{array} \right) = M(-\theta) \left( M(\theta) \left( \begin{array}{c} u \\ v \\ \end{array} \right) \right) \)
となります。少し面倒ですが、元々の \(M\) を使わない式まで戻ってこれを計算すると、\(M(\theta)\) の計算と \(M(-\theta)\) の計算が相殺することで、
\( \left( \begin{array}{c} u \\ v \\ \end{array} \right) = M(-\theta) \left( \begin{array}{c} u^\prime \\ v^\prime \\ \end{array} \right) \)
となることが分かります。これが、座標系 \(E\) での座標を座標系 \(G\) での座標に変換する式です。
ここで注意があります。
上の説明では、座標系 \(G\) での座標を座標系 \(E\) での座標に変換する際は、回転の幾何学的な考察から計算式を導きました。その一方、\(E\) での座標を \(G\) での座標に変換する際は、計算だけで変換式を導きました。
実は、2次元の回転の場合は、\(E\) から \(G\) に乗り換えると、平面上の図形が角 \(-\theta\) の回転をするように見えることから、幾何学的な考察で座標の変換式を導くことができます。しかし、同じことを3次元の回転でやろうとすると、恐らく、ほとんどの人は訳が分からなくなると思います。
ここでは、座標に対して \(M(\theta)\) の計算を行った後、続けて \(M(-\theta)\) の計算を行った場合、双方が相殺して、何も計算しないのと同じ結果になる、ということを覚えておいてください。
右手系
3次元の回転を考える準備として、右手系について説明しておかなければなりません。
2次元空間に座標系を設置する場合、特に理由がなければ、左右方向の右向きに x 軸を、上下方向の上向きに y 軸をとるのが慣習になっています。このとき、この平面に対して手前の向きに z 軸をとった座標系を右手系と呼びます。逆に、奥の向きに z 軸をとると左手系になります。
ある3次元直交座標系が右手系であるかどうかを確かめるのに、回転とねじの進む向きを考える方法があります。
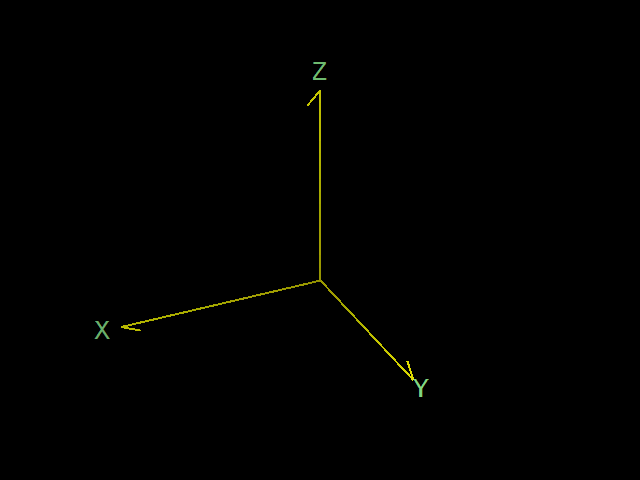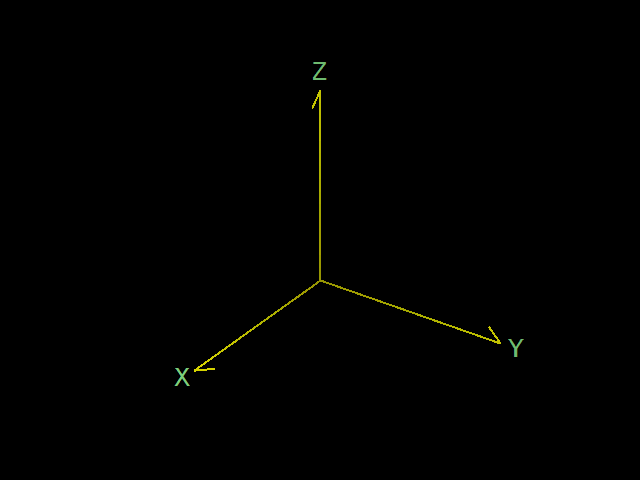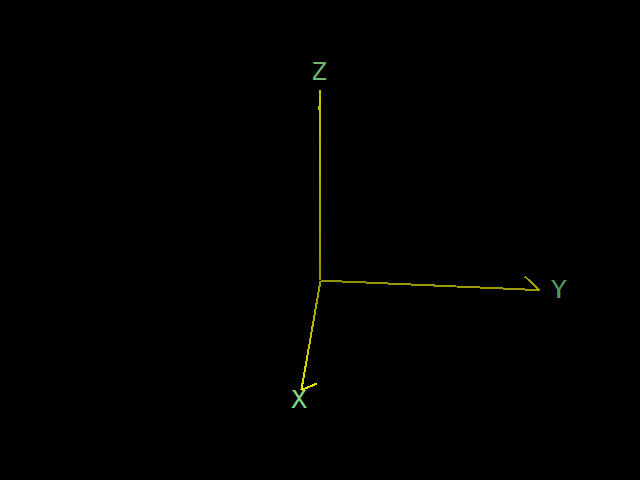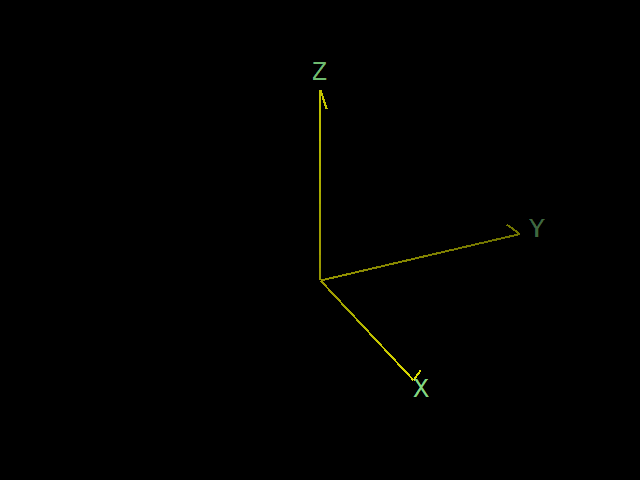
上の図の直交座標系で、x 軸を y 軸に近づけるように回転させることを考えます。この回転の動作を手首を使って実際にやってみてください。その回転の動作でねじを回すと、ねじが進んで締まります。ビンの蓋などもこの向きで締まります。よほど特殊な目的のねじや蓋でない限り、普通はそうなっているはずです。
このとき、z 軸の向きが、ねじや蓋の進む向きと同じであれば、その座標系は右手系です。
この関係は、x、y、z を循環させても変わりません。
つまり右手系では、y 軸を z 軸に近づけるように回したとき、x 軸はねじの進む向きを向いています。z 軸を x 軸に近づけるように回したとき、y 軸はねじの進む向きを向いています。
3次元の回転
右手系について理解していれば、3次元空間での回転の定義は簡単です。
右手系をなす3次元直交座標系での z 軸周りの回転を考えます。このとき、ねじを z 軸の正の向きに進める回転を、z 軸周りの正の角の回転、とします。逆に、ねじを z 軸の負の向きに進める回転は、負の角の回転、ということです。
図形を z 軸周りに角 \(\theta\) だけ回転させる操作を \(\hat{R}_z(\theta)\) と書くことにします。
x 軸周りや y 軸周りの回転についても同じように定義し、それぞれの回転操作を \(\hat{R}_x(\theta)\)、\(\hat{R}_y(\theta)\) と書きます。
各軸の回転を定義したので、それぞれの回転操作で、点の座標がどのように変化するかを調べておきます。
まず、点 \(P\) を z 軸の周りに角 \(\theta\) 回転させる場合について考えます。
\( P^\prime = \hat{R}_z (\theta) \, P \)
この場合の座標の計算式は2次元の回転の場合とほぼ同じです。ただし、z 軸周りの回転では、点の z 座標が変化しないことを式に書き加えておかなければなりません。
回転前の点 \(P\) の座標を \((x,y,z)\)、回転後の \(P^\prime\) の座標を \((x^\prime,y^\prime,z^\prime)\) とすると、
\( \left\{ \begin{array}{l} x^\prime = x \cos\theta \,\, – \,\, y \sin\theta \\ y^\prime = x \sin\theta \, + \, y \cos\theta \\ z^\prime = z \\ \end{array} \right. \)
となります。これを例によって、
\( \left( \begin{array}{c} x^\prime \\ y^\prime \\ z^\prime \\ \end{array} \right) = M_z(\theta) \left( \begin{array}{c} x \\ y \\ z \\ \end{array} \right) \)
という形に書き換えておきます。\(M_z(\theta)\) は回転後の座標を計算する操作を表します。
x 軸周りと y 軸周りの回転についての計算式は、z 軸の場合の計算式の中で、x、y、z を循環させることで得られます。これらの計算の操作も、それぞれ、\(M_x(\theta)\)、\(M_y(\theta)\) で表します。
本文でも述べたように、z 軸周りの回転は2次元の回転とほぼ同じです。そのため、以前に書いた2次元の回転用のコードを次のように呼び出すことで座標を計算できます。
rotate(ref x, ref y, radian); // z 軸周りの回転。
回転によって x 座標と y 座標は変化しますが、z 座標は変化しません。
x 軸周り、y 軸周りの回転の場合は、x、y、z を循環させた式で座標を計算できるので、
rotate(ref y, ref z, radian); // x 軸周りの回転。
rotate(ref z, ref x, radian); // y 軸周りの回転。
と関数を呼び出せばよいことになります。
ここで、x、y、z は循環させなければならないので、並び順を変えてはいけません。例えば、y 軸周りの回転で
rotate(ref x, ref z, radian); // y 軸周りの逆回転。
とすると、回転の向きが逆になってしまいます。
3次元の回転を表す式は、例えば z 軸周りの回転の場合、行列を使って
\( \left( \begin{array}{c} x^\prime \\ y^\prime \\ z^\prime \\ \end{array} \right) = \left( \begin{array}{ccc} \cos\theta & -\sin\theta & 0 \\ \sin\theta & \cos\theta & 0 \\ 0 & 0 & 1 \\ \end{array} \right) \left( \begin{array}{c} x \\ y \\ z \\ \end{array} \right) \)
と書くことができます。これを計算するには線形代数の知識が必要になります。x 軸周りや y 軸周りの回転についても3×3行列を使って似たような書き方ができます。
しかし、そのような表記は、学生のレポート課題でもない限り、あまり実用性がありません。コンピューターを使う場合、x、y、z 軸周りの回転は、2次元の回転と同じコードで計算ができてしまうからです。
3次元空間では、いろいろな向きの軸の周りの回転を考えることができ、それらを組み合わせることができます。
例えば、3次元空間中の図形 \(S\) を、x 軸の周りに \(\pi\)/2 回転させ、その結果をさらに y 軸の周りに \(\pi\)/2 回転させることを考えてみます。これは、式で書くと
\( S^\prime = \hat{R}_y(\pi/2) \left( \hat{R}_x(\pi/2) \, S \right) \)
となります。
このように、いくつかの操作を連続して行う場合、数学では
\( S^\prime = \hat{R}_y(\pi/2) \, \hat{R}_x(\pi/2) \, S \)
のように括弧を省略して書き、右から順番に操作を行う、とすることが多いです。
ここで、3次元の回転では、操作の順序を入れ替えると結果が変わることに注意してください。これは、上の例では、
\( \hat{R}_y(\pi/2) \, \hat{R}_x(\pi/2) \neq \hat{R}_x(\pi/2) \, \hat{R}_y(\pi/2) \)
ということです。この式による回転の様子を図にすると下のようになります。
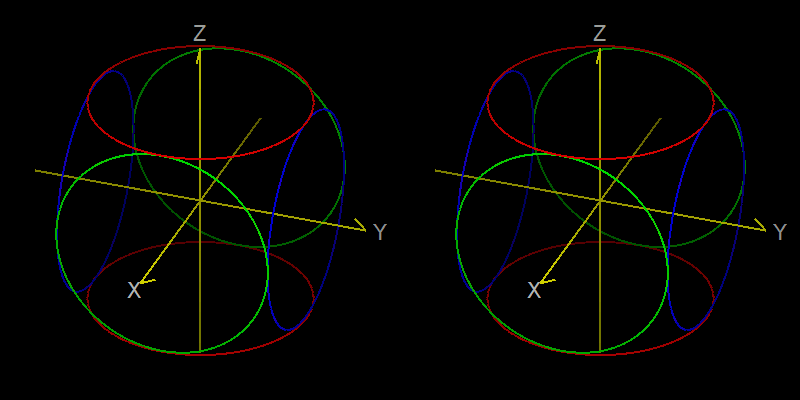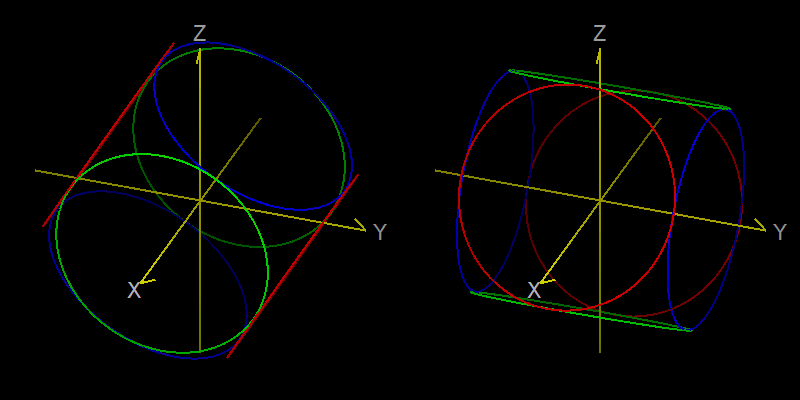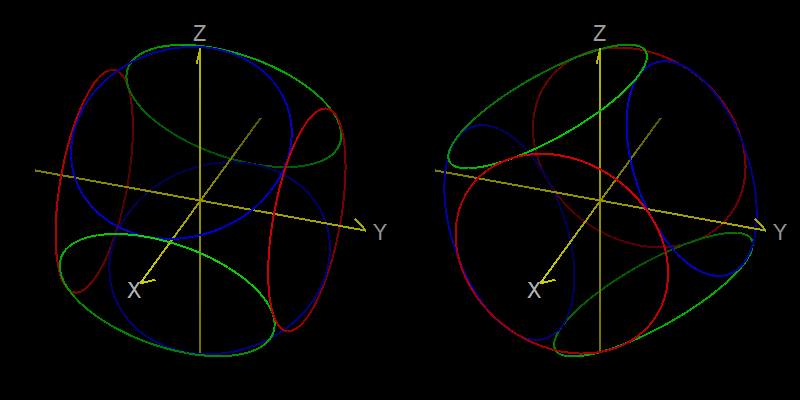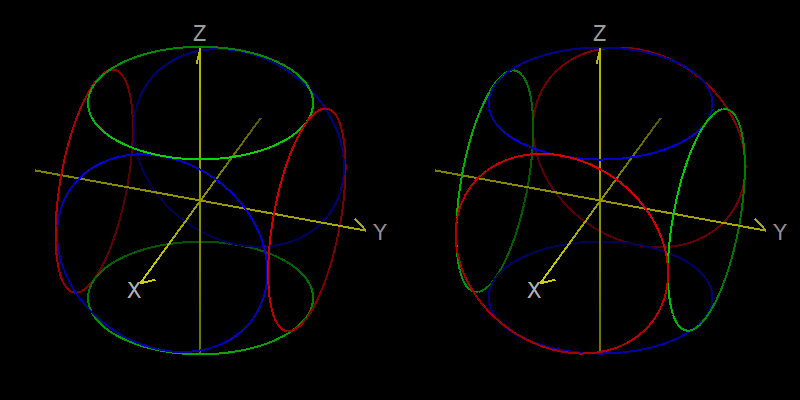
回転の順序を変えることで、結果が異なった図形になることが分かります。
3次元空間では、座標軸の周りの回転だけではなく、任意の向きの軸について、その周りの回転を考えることができます。しかし、その場合、座標の計算などはかなり面倒なものになります。
そこで、任意軸の周りの回転を扱う場合は、その回転を座標軸の周りの回転に分解できないかを考えます。
赤道座標と銀河座標
赤道座標と銀河座標は、どちらも、球面座標の一種です。
直交座標系 \(E\) が設置された3次元空間で、原点を中心とする球面を考えます。この球面上に赤道座標系を設置します。まず、天の北極が z 軸方向の正の向き、南極が負の向きになるようにします。次に、春分点が x 軸方向の正の向きになるようにします。
このように赤道座標系を設置すると、天体の赤経 \(\alpha\) は x-y 平面上で x 軸方向正の向きからの角として、赤緯 \(\delta\) は天体の方向と x-y 平面がなす角として測ることができます。
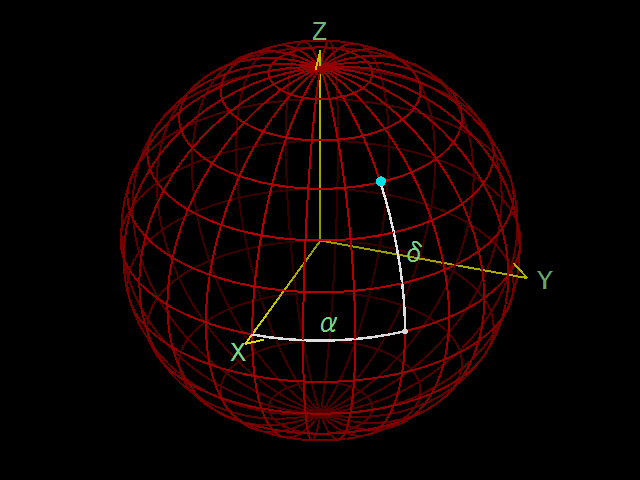
赤道座標と銀河座標の関係ですが、銀河北極は赤道座標系から見て赤経 \(\alpha_G\)、赤緯 \(\delta_G\) にあり、銀河座標から見た天の北極の銀経は \(l_{NCP}\) となっています。
Wikipedia のこの記事 によると、J2000.0 分点では、これらの角度パラメーターの値は、それぞれ、
\(\alpha_G\) = 192.85948° 、 \(\delta_G\) = 27.12825° 、 \(l_{NCP}\) = 122.93192°
とされています。
3次元空間中の図形 \(S\) が赤道座標系の経線と緯線だとします。上に与えられた角を使って、赤道座標系の経線と緯線を回転させることで、銀河座標系の経線と緯線 \(S^\prime\) と一致させることを考えます。これは次の手順で行えます。
1:まず、\(S\) を z 軸周りに \(\pi-l_{NCP}\) 回転させます。
2:次に、y 軸周りに \(\pi/2-\delta_G\) 回転させます。
3:最後に、もう一度 z 軸周りに \(\alpha_G\) 回転させます。
この回転の様子を下の図に示します。ただし、この図は見やすさのために、実際の角度パラメーターとは異なった回転角を使っています。
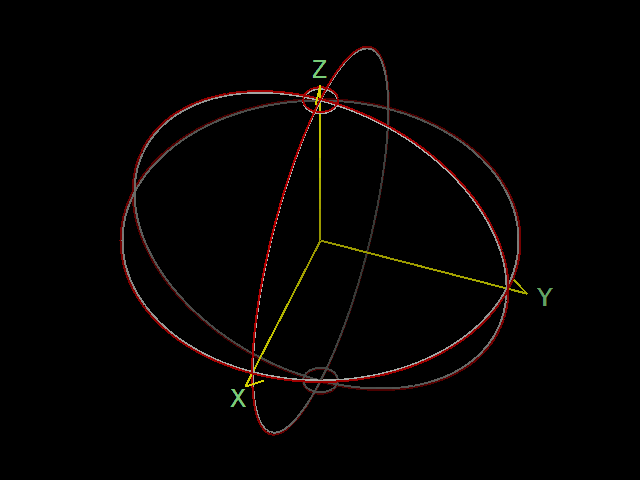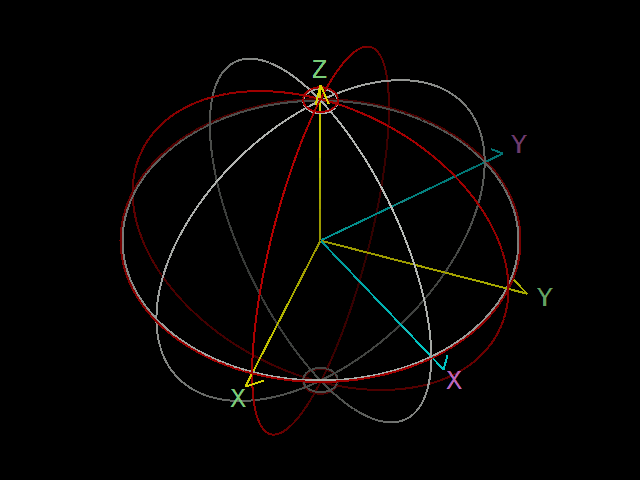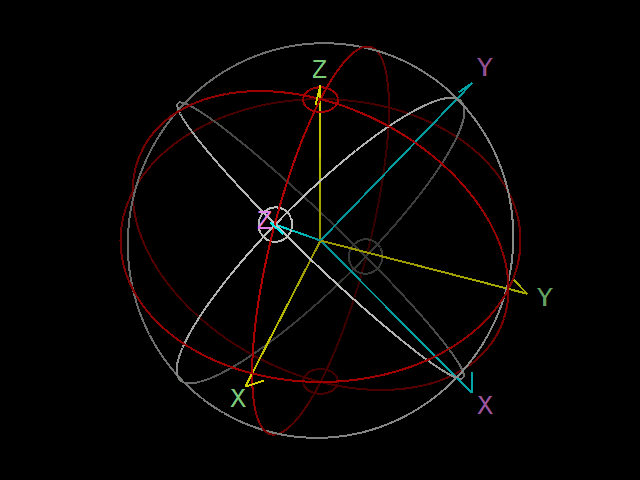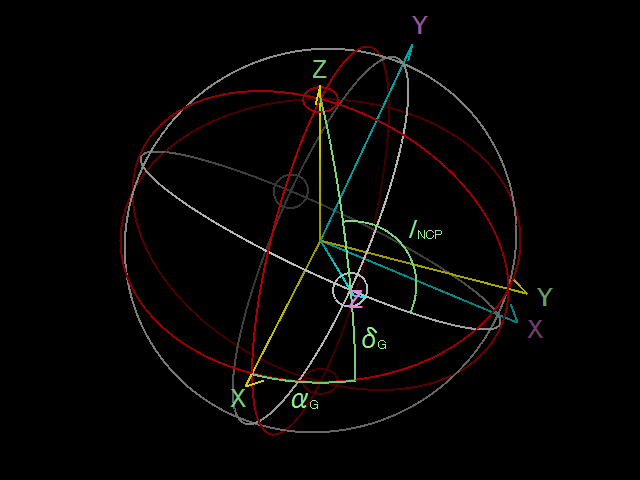
これで、赤道座標系の経線と緯線 \(S\) を回転させたものは、銀河座標系の経線と緯線 \(S^\prime\) に一致しました。つまり、
\( S^\prime = \hat{R}_z(\alpha_G) \, \hat{R}_y(\pi/2-\delta_G) \, \hat{R}_z(\pi-l_{NCP}) \, S \)
ということです。
図形 \(S\) として、直交座標系 \(E\) の座標軸をとり、これに上と同じ回転操作を施してできた図形 \(S^\prime\) を座標軸とする直交座標系を \(G\) とします。
この回転の操作による3次元空間中の点 \(P\) の座標の変化を計算します。直交座標系 \(E\) での点 \(P\) の回転前の座標を \((x,y,z)\)、回転後の座標を \((x^\prime,y^\prime,z^\prime)\) とすると、これは
\( \left( \begin{array}{c} x^\prime \\ y^\prime \\ z^\prime \\ \end{array} \right) = M_z(\alpha_G) \, M_y(\pi/2-\delta_G) \, M_z(\pi-l_{NCP}) \left( \begin{array}{c} x \\ y \\ z \\ \end{array} \right) \)
となります。
2次元での回転を考えた時と同様に考えると、これが、直交座標系 \(G\) での座標 \((x,y,z)\) を直交座標系 \(E\) での座標 \((x^\prime,y^\prime,z^\prime)\) に変換する座標変換の式となります。
逆に、直交座標系 \(E\) での座標 \((x^\prime,y^\prime,z^\prime)\) を直交座標系 \(G\) での座標 \((x,y,z)\) に変換する式を導くには、この式の両辺に、\( M_z(l_{NCP}-\pi) \, M_y(\delta_G-\pi/2) \, M_z(-\alpha_G) \) という計算の操作を施します。すると、座標変換の式として
\( \left( \begin{array}{c} x \\ y \\ z \\ \end{array} \right) = M_z(l_{NCP}-\pi) \, M_y(\delta_G-\pi/2) \, M_z(-\alpha_G) \left( \begin{array}{c} x^\prime \\ y^\prime \\ z^\prime \\ \end{array} \right) \)
が得られます。ここで、\(M(\theta)\) という計算操作を行った直後に \(M(-\theta)\) の計算操作を行うと、双方が相殺することを使いました。
2次元の回転のところで述べたように、直交座標系 \(G\) から直交座標系 \(E\) への座標変換は、回転を幾何学的に考えることで理解できると思います。しかし、逆変換については、計算のみに頼ったほうが分かりやすいでしょう。
まず、座標変換に関係する角度を弧度法に変換しておきます。
private double alpha_G = 192.85948;
private double delta_G = 27.12825;
private double l_NCP = 122.93192;
private void calculateParameterRadian()
{
alpha_G = degreeToRadian(alpha_G);
delta_G = degreeToRadian(delta_G);
l_NCP = degreeToRadian(l_NCP);
}
上のコードでは、いくつかの関数で共通して使う角度パラメーターを、関数の外側で宣言しています。
変換した角を使って直交座標系 \(G\) の座標を直交座標系 \(E\) の座標に変換するには、次のようなコードを使えばよいでしょう。
private void transformGtoE(ref double x, ref double y, ref double z)
{
rotate(ref x, ref y, Math.PI - l_NCP); // z 軸周りの回転。
rotate(ref z, ref x, Math.PI / 2.0 - delta_G); // y 軸周りの回転。
rotate(ref x, ref y, alpha_G); // z 軸周りの回転。
}
逆変換は、
private void transformEtoG(ref double x, ref double y, ref double z)
{
rotate(ref x, ref y, -alpha_G); // z 軸周りの回転。
rotate(ref z, ref x, delta_G - Math.PI / 2.0); // y 軸周りの回転。
rotate(ref x, ref y, l_NCP - Math.PI); // z 軸周りの回転。
}
とすればよいでしょう。
これらのコードでは、alpha_G のような角度パラメーターが、関数外で定義されていることに注意してください。
これで、直交座標系 \(E\) と直交座標系 \(G\) との座標変換が分かりました。あとは、球面座標と直交座標の関係を知ることで、球面座標系の間の座標変換が行えるようになります。
今、直交座標系 \(E\) に関連付けられた赤道座標系から見て、ある天体が赤経 \(\alpha\)、赤緯 \(\delta\) にあるとします。これが半径1の球面にあるとすると、その直交座標系 \(E\) での座標は
\( \left( \begin{array}{c} x^\prime \\ y^\prime \\ z^\prime \\ \end{array} \right) = \left( \begin{array}{c} \cos\delta \cos\alpha \\ \cos\delta\sin\alpha \\ \sin\delta \\ \end{array} \right) \)
となります。この関係から、逆に、赤経 \(\alpha\) と赤緯 \(\delta\) は、それぞれ、
\( \delta = \arcsin z^\prime \) 、 \( \alpha = \arctan \frac{y^\prime}{x^\prime} \)
で計算することができます。ここで、\(\arcsin x\) と \(\arctan x \) は、それぞれ、\(\sin x\) と \(\tan x\) の逆関数です。
直交座標系 \(G\) での座標 \((x,y,z)\) と、\(G\) に関連付けられた銀河座標系での銀経 \(l\) と銀緯 \(b\) についても同様の式が成立します。
直交座標と球面座標の間の変換を行うコードを考えます。球面座標から直交座標への変換は簡単で、例えば、赤道座標から直交座標へは次のコードで変換できます。
private void toOrthogonal(ref double x, ref double y, ref double z, double alpha, double delta)
{
x = Math.Cos(delta) * Math.Cos(alpha);
y = Math.Cos(delta) * Math.Sin(alpha);
z = Math.Sin(delta);
}
一方、直交座標から球面座標への変換には、ちょっとした配慮が必要になります。次のコードを見てください。
private void toSpherical(ref double alpha, ref double delta, double x, double y, double z)
{
if(Math.Abs(x) > Math.Abs(y)) // Math.Abs(x) は x の絶対値です。
{
alpha = Math.Atan(y / x); // Math.Atan(x) は \(\arctan x\) です。
if(x < 0.0) { alpha += Math.PI; }
if(alpha < 0.0) { alpha += 2.0 * Math.PI; }
}
else
{
alpha = Math.PI / 2.0 - Math.Atan(x / y);
if(y < 0.0) { alpha += Math.PI; }
}
delta = Math.Asin(z); // Math.Asin(x) は \(\arcsin x\) です。
}
\(\delta\) の計算は簡単ですが、\(\alpha\) の計算については4つの場合に分けています。これは、\(\theta = \arctan x\) の値域が \( -\pi/2 < \theta < \pi/2 \) であることと、Atan 関数の引数が発散しないよう考慮しているためです。
\(\delta\) の計算についても、球面座標系の北極や南極に非常に近い場合は、誤差により z の絶対値が1を超え、エラーとなることがあり得ます。
この記事でこれまでに解説した知識を使えば、赤道座標から銀河座標への座標変換を具体的に計算できるはずです。
手順としては、まず、赤道座標の赤経と赤緯から、3次元空間中の直交座標を計算します。これを、赤道座標系と銀河座標系の回転関係に従って回転座標変換します。最後に、回転座標変換後の直交座標から銀河座標を計算します。
赤道座標と銀河座標以外の球面座標間の座標変換でも、考え方は同じです。
これまでに示したサンプルコードを使って、赤道座標から銀河座標への座標変換のコードを書いてみます。
以下のコードでは、時間表記の赤経 \(\alpha\) と度数法の赤緯 \(\delta\) を、度数法の銀経 \(l\) と銀緯 \(b\) に変換します。変換に必要な \(\alpha_G\) などのパラメーターは度数法で与えられているものとします。
private double alpha_G = 192.85948;
private double delta_G = 27.12825;
private double l_NCP = 122.93192;
private void sample()
{
double l = 0.0; double b = 0.0; // 計算結果を受け取る銀経銀緯。
calculateParameterRadian(); // パラメーターを弧度法に変換。
double alpha = dmsToDegree(6.0, 45.0, 9.2499); // シリウスの赤経赤緯。
double delta = dmsToDegree(-16.0, -42.0, -47.315);
equatorialToGalactic(ref l, ref b, alpha, delta); // 赤道座標を銀河座標に変換。
// 計算結果は l = 227.22816034 、 b = -8.88779424 。
// 実際の値は l = 227.22815779 、 b = -8.88779558 。
}
private void equatorialToGalactic(ref double l, ref double b, double alpha, double delta)
{
double x = 0.0; double y = 0.0; double z = 0.0; // 作業用の直交座標。
alpha = hourToRadian(alpha); // 赤経赤緯を弧度法に変換。
delta = degreeToRadian(delta);
toOrthogonal(ref x, ref y, ref z, alpha, delta); // 赤道座標を直交座標Eに変換。
transformEtoG(ref x, ref y, ref z); // EからGへの回転座標変換。
toSpherical(ref l, ref b, x, y, z); // 直交座標Gを銀河座標に変換。
l = radianToDegree(l); // 銀経銀緯を度数法に変換。
b = radianToDegree(b);
}
このサンプルコードは、何らかのクラスの一部として実装しなければ動作しません。計算のアルゴリズムを学ぶための参考にしてください。
シリウスの座標は Hipparcos Main Catalog の値を用いています。
計算結果とデータベースの値は7桁目で一致しませんが、計算に使っているパラメーターの精度が7桁程度なので、十分に正確な計算ができていると言えるでしょう。
この記事では、赤道座標のような球面座標を、いちど3次元空間の直交座標に変換する、という手法で球面座標間の座標変換を考えました。しかし、この方法は必ずしも、最も簡単な計算手法、というわけではありません。
例えば、赤道座標系を天の北極と南極を通る軸の周りに回転させる場合の座標変換を考えます。この場合、赤経の変換は、赤経と回転角との和や差で簡単に計算できます。
このように、工夫をすれば、この記事で説明した手法よりも簡単な計算手法はあり得ます。
しかし、コンピューターを使って座標計算を行う場合、それほど大きな計算時間の差は出ないでしょうし、倍精度変数を使えば、計算の誤差も実用上の問題とはならないでしょう。
そこでこの記事では、計算を簡単にすることよりも、統一した考え方で座標変換の計算手順を導き出すことに主眼を置きました。この考え方を理解すれば、いろいろな球面座標間の座標変換に応用できるでしょう。
下の記事は、この記事の内容の応用例です。



