夜空には、赤い星や黄色い星、青白い星など、いろいろな色の恒星が見られます。私は趣味で、天文学的なデータからゲーム用の星空のテクスチャーを作ったことがあります。この記事では、そのテクスチャーの作成で使った、恒星の色の RGB 値を計算する方法についてまとめておきます。
恒星に限らず、高温の物体は光を放ちます。この記事の解説は、そのような光の色の計算にも応用できると思います。
恒星の温度の推定
恒星の光の観測は、光の強度を測定するセンサーと、特定の波長の光を通すフィルターを組み合わせることで、いくつかの波長域(バンド)で行われます。
このうち、人の眼で見ることのできる可視光の範囲では、青色の光を透す B、緑色から黄色にかけての光を透す V、赤色の光を透す R のフィルターが使われます。このほか、人の眼では見えない範囲の電磁波の観測には、紫外線を透す U、赤外線を透す I などのフィルターが使われます。
恒星の色を計算するには、まず、これらのうちの2つの波長域で測定された恒星の明るさから、恒星の絶対温度を推定しなければなりません。いくつかの方法があるようですが、通常の恒星の温度推定では、B バンドと V バンドの明るさの比から計算される B-V 色指数を使う方法が幅広く用いられています。
これは次のような方法です。まず、理論的に正確に計算できる黒体放射のスペクトルについて、様々な温度で B-V 色指数を計算しておきます。これにより、絶対温度 \(T\) の関数としての B-V 色指数 \(M_{BV}(T)\) が得られます。恒星の絶対温度は、観測した B-V 色指数から \(M_{BV}(T)\) の逆関数である \(T(M_{BV})\) を使って推定します。
この \(T(M_{BV})\) については、次のような近似式が知られています。
\( T = 4600 \left( \displaystyle \frac{1}{0.92 \, M_{BV} + 1.7} + \frac{1}{0.92 \, M_{BV} + 0.62} \right) \)
CIE 1931 色空間
人間の眼の網膜には、通常3種類の、錐体細胞と呼ばれる光を知覚する組織があります。これら3種類の錐体細胞は、それぞれ、感知する光の波長域が異なっています。
つまり、私たち人間は、様々なスペクトルの光を3次元空間にマッピングしているのです。そして、この3次元空間中で位置の異なる光を、異なった色、として知覚しているのです。この3次元空間を色空間と呼びます。
人間の知覚する色を3次元空間にマッピングする場合、必ずしも、座標軸として錐体細胞の刺激値を使うのが便利とは限りません。例えば、色相、彩度、明度といった、別の座標軸を使ったほうが便利な場合があります。このように、錐体細胞の刺激値を座標軸とする色空間と、応用上より便利な座標軸をもつ色空間は、3次元の座標変換で繋がっていて、目的によって使い分けることができます。
私たちの生活では、印刷やカメラ、モニター画面など、様々なところで色は重要な役割を果たします。そこで、国際照明委員会(CIE)によって定められた色空間のひとつが CIE 1931 XYZ 色空間です。
この色空間は、上で述べた通り、3次元空間なのですが、恒星の色について計算するには、輝度を考えに含めない空間を考える必要があります。輝度の自由度が減るので、これは2次元空間で、それを図示したものが CIE xy 色度図です。
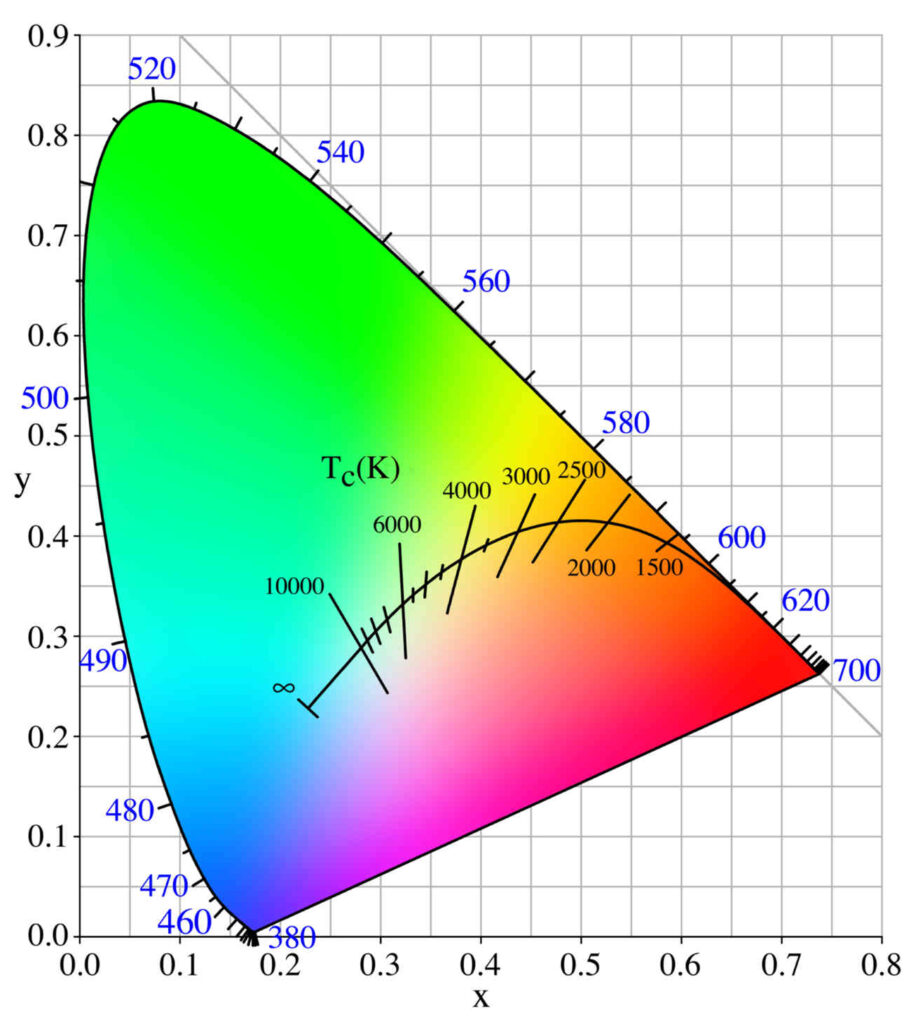
この色度図での座標 \((x,y)\) と黒体放射のスペクトルの関係を知ることができれば、黒体放射の絶対温度 \(T\) を媒介として、恒星の B-V 色指数を色に変換できます。
かなり細かい数字が出てきますが、この \(T\) と \((x,y)\) の関係については、次の近似式が知られています。
\( t = 10^3 / \, T \)
\( x = \left\{ \begin{array}{ll} -0.2661239 \, t^3 \,\, – \,\, 0.2343589 \, t^2 + 0.8776956 \, t + 0.179910 & (1667 \, \mbox{K} \leq T \leq 4000 \, \mbox{K}) \\ -3.0258469 \, t^3 + 2.1070379 \, t^2 + 0.2226347 \, t + 0.240390 & (4000 \, \mbox{K} \leq T \leq 25000 \, \mbox{K}) \\ \end{array} \right. \)
\( y = \left\{ \begin{array}{ll} -1.1063814 \, x^3 \,\, – \,\, 1.34811020 \, x^2 \, + \, 2.18555832 \, x \,\, – \,\, 0.20219683 & (1667 \, \mbox{K} \leq T \leq 2222 \, \mbox{K}) \\ -0.9549476 \, x^3 \,\, – \,\, 1.37418593 \, x^2 \, + \, 2.09137015 \, x \,\, – \,\, 0.16748867 & (2222 \, \mbox{K} \leq T \leq 4000 \, \mbox{K}) \\ +3.0817580 \, x^3 \,\, – \,\, 5.87338670 \, x^2 \, + \, 3.75112997 \, x \,\, – \,\, 0.37001483 & (4000 \, \mbox{K} \leq T \leq 25000 \, \mbox{K}) \\ \end{array} \right. \)
sRGB 色空間
上で計算した CIE xy 色度図での座標 \((x,y)\) から、モニターなどに色を表示するための RGB 値を計算するのですが、これは、2次元空間から3次元空間への変換になります。これを行うには、まず、座標 \((x,y)\) を、下の式で元の3次元空間の座標 \((X,Y,Z)\) に戻します。
\( Y = 1 \) \( X = \displaystyle \frac{Y}{y} x \) \( Z = \displaystyle \frac{Y}{y} (1-x-y) \)
この式で \( Y = 1 \) となるのは、元々 \(Y\) に輝度の意味があり、これを一定として色度図を作ったからです。
この \((X,Y,Z)\) から RGB 値を計算するのですが、その変換式は、作成した画像を表示させるデバイスが、どれほどの範囲の色を表現できるかによって異なります。ここでは下に示す線形変換で、ウェブページなどで標準とされている sRGB 色空間に変換します。
\( \left( \begin{array}{c} R \\ G \\ B \\ \end{array} \right) = \left( \begin{array}{ccc} +3.2406 & -1.5372 & -0.4986 \\ -0.9689 & +1.8758 & +0.0415 \\ +0.0557 & -0.2040 & +1.0570 \\ \end{array} \right) \left( \begin{array}{c} X \\ Y \\ Z \\ \end{array} \right) \)
CIE 1931 XYZ 色空間から sRGB 色空間への変換についての解説を見ると、上の線形変換で計算された RGB 値に対し、更にガンマ補正を行ったり、RGB 値を0から1の範囲に収めたり、といった操作を行うようです。そして、最終的には、モニターなどに表示させる RGB の輝度を計算します。
しかし、私が星空のテクスチャーを作った際には、この段階で、あまり標準的ではない処理を行いました。
これは、このテクスチャーの使途がゲームであり、科学的、技術的な正確さよりも、見た目の綺麗さが重要と考えたためです。
計算例
ここでは、Hipparcos Main Catalog のデータを使って、オリオン座のリゲルとベテルギウスの色を計算します。
データベースでは、これらの恒星の明るさと色は、次のように記述されています。
|ra |dec |vmag |bv_color|
|05 14 32.2712|-08 12 05.901| 0.18| -0.030|
|05 55 10.2892|+07 24 25.331| 0.45| 1.500|
2行目がリゲル、3行目がベテルギウスについてのデータです。ra と dec は恒星の座標、vmag は等級で、bv_color が RGB 値を計算するための B-V 色指数です。
上で説明した手順に従って計算すると、それぞれ、次のような計算結果が得られます。
リゲル
bv_color = -0.030
T kelvin = 10515.5
(x,y) = (0.27801, 0.28510)
(X,Y,Z) = (0.97511, 1.00000, 1.53230)
(R,G,B) = (0.85874, 0.99460, 1.46996)
ベテルギウス
bv_color = 1.500
T kelvin = 3793.5
(x,y) = (0.39011, 0.38255)
(X,Y,Z) = (1.01977, 1.00000, 0.59423)
(R,G,B) = (1.47118, 0.91240, 0.48091)
リゲルとベテルギウスの絶対温度は、それぞれ、10516 K、3794 K と計算されました。
ここで計算された RGB 値を使ってモニターなどに表示する RGB の輝度を計算します。標準的には、ここでガンマ補正を行ったり、数値を0から1の範囲に収めたうえで、デバイスが表示可能な輝度に変換します。
しかし、ここで私は、以下のような計算を行いました。
まず、計算された RGB 値のうち、最も大きいものが 255 になるようにスケールします。これにより、リゲルの色は #95ADFF、ベテルギウスの色は #FF9E53 となります。

次に、恒星をスクリーン上で円形に描くのですが、この段階で、円の中心に近い部分で輝度を足すことで、白っぽい色になるようにしました。具体的には、各 RGB 値を次の式で持ち上げます。
\( L_{b} = (1-b) L + 255 \, b \)
調整前の RGB 値が \(L\)、調整後の RGB 値が \(L_{b}\) です。\(b\) は0から1の間の値をとるパラメーターで、これにより各 RGB 値は \(255\,b\) だけ持ち上がることになります。
このような処理を行ったのは、次のような考えによるものです。
私たちが星空を頭の中で思い浮かべるとき、そのイメージは必ずしも肉眼で見たものではありません。私たちは日常のいろいろな場面で、星空の映像に接しています。そのような映像は、多くの場合、カメラの長時間露光で撮影したものです。長時間露光によって、肉眼では見えない暗い星まで撮影することができるのです。
その一方、明るい恒星は露出オーバーになります。そのような露出オーバーに撮影された恒星は色が白く潰れて見えるでしょう。
私たちは、知らず知らずのうちに、そのような映像に慣らされているのではないか、と考えたのです。その場合、恒星の明るい部分の色を少し白く潰したほうが、私たちが頭の中で描く星空のイメージに近くなるはずです。
科学の世界では、観測データやシミュレーション結果を映像にする可視化(visualization)という手法が用いられます。これは、数値の羅列では分かりにくい現象を、直感的に分かりやすくするもので、研究を進める段階でも、研究成果を公表する段階でも行われます。
その際、特に研究成果を公表する場合には、科学的に正確なだけでは、美しくアピールできるような映像を作れなかったりします。科学的な正確さを犠牲にせず、いかにアピールできる映像を作るかは、難しく悩ましい問題です。
この記事で解説した方法で作ったテクスチャーは、以下の記事で紹介しています。



