日本の学校では、負の数について中学1年生で学びます。そのなかで、負の数と負の数を掛けあわせると正の数になることを教わります。
これがなぜなのかが、大人になっても分からない、という人もいるようです。
そっけなく答えるならば、負の数×負の数=正の数 というのを ルール にしておくと、いろいろと便利だから、ということになります。
数学は世の中のあらゆるところで使われています。そのような現実の問題を考えるとき、すべてを一から考えていると大変なことになります。そこで、いろいろな問題で共通する考え方をルールにしてしまえば、考える労力を大幅に減らすことができます。
ところが、ルールだけを教わったり暗記したりすると、当然のことながら、なぜ、そのルールが成り立つのかを考える機会はなくなってしまいます。
この記事では、なぜ、負の数×負の数=正の数 になるのかを、数の向き を考えることで解説してみたいと思います。
私はもともと科学者だったので、この記事の内容は、科学者から見た解説になっていると思います。数学者は、この記事とは違った解説をするかもしれませんね。
数直線と足し算、引き算
数直線については小学校で習っていると思います。左端に 0 があり、右に向かって、1、2、3…、と大きな数が続いてゆきます。この線上の位置で数を表します。
例えば、2 という数は、数直線の左端の0の位置に点を置き、これを2つ右に動かした位置で表すことができます。
ここではまず、足し算と引き算について、数直線を使うとどのようなイメージになるかを見ていきます。
例として、2+3=5 という計算について、数直線を使って考えてみます。
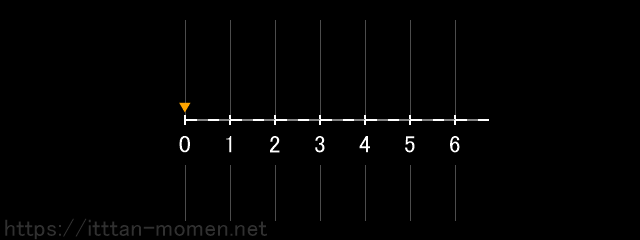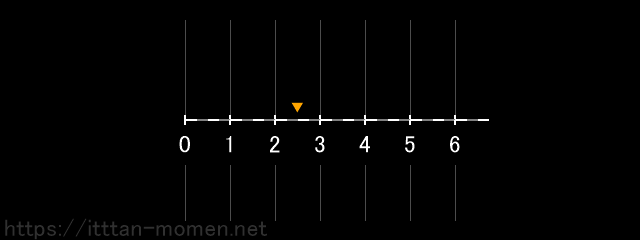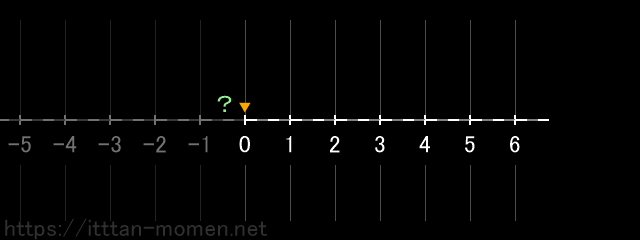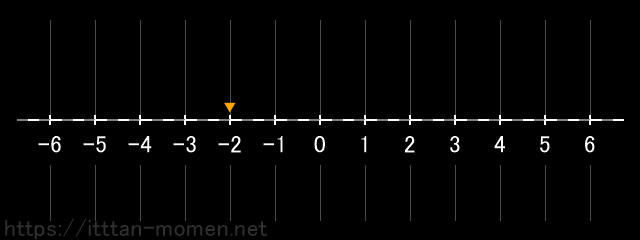
まず、点を0の位置に置き、これを2つ右に動かします。
次に、その点をさらに3つ右に動かします。
すると、結果として、点は5の位置にきます。
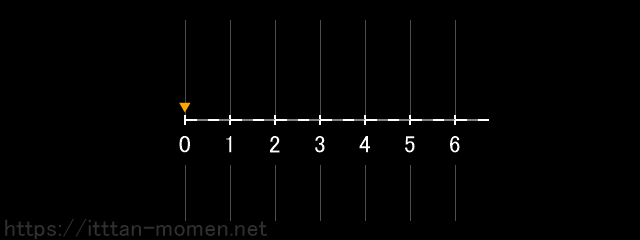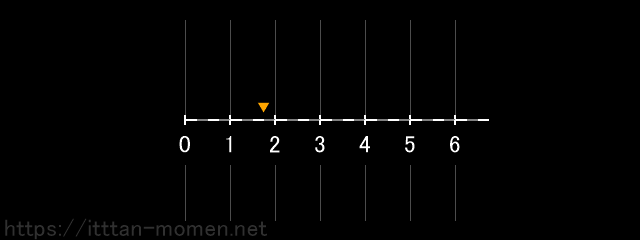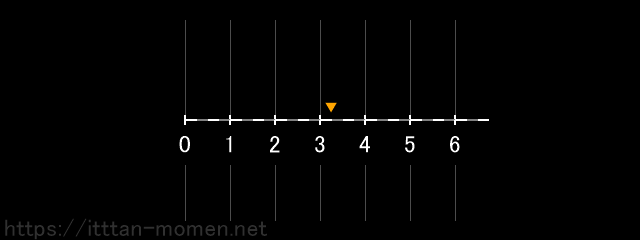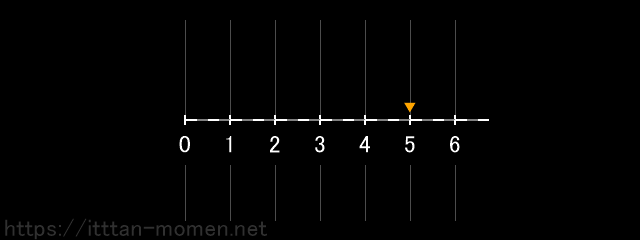
これが、2+3=5 という計算の数直線でのイメージです。
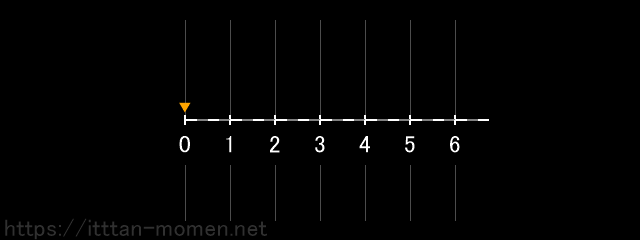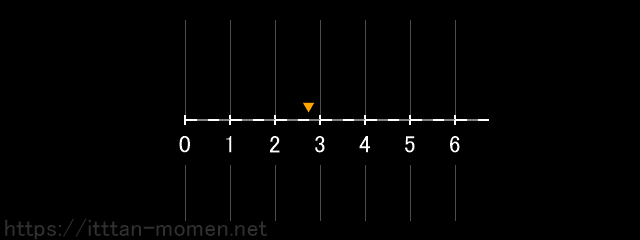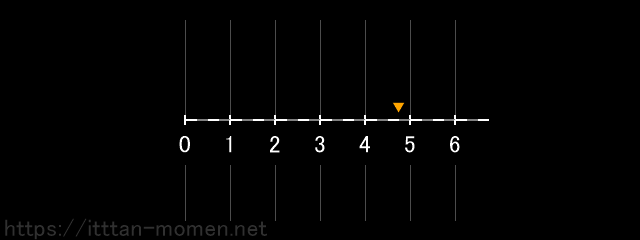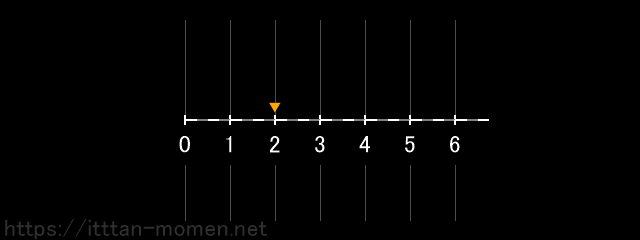
続いて、5-3=2 という計算について、同じように数直線を使って考えてみます。
まず、点を0の位置に置き、これを5つ右に動かします。
次に、その点を3つ左に動かします。
すると、結果として、点は2の位置にきます。
これが、5-3=2 という計算の数直線でのイメージです。
つまり、足し算や引き算は、数直線上では、点を左右に移動させることであり、足し算の場合は点を右向きに、引き算の場合は点を左向きに動かすことになるのです。
ここで、3-5 という計算について考えてみます。
まず、点を0の位置に置き、これを3つ右に動かします。
次に、その点を5つ左に動かしたいのですが…。
小学校までの算数の範囲では、ここで困ったことが起こります。3の位置にある点を5つ左に動かそうとすると、0の位置を突き破って、さらに2つ左に動かさなければならなくなります。
ここでどうするかが運命の分かれ道なのですが、0 より小さい数って何、などといった常識にはとらわれず、思い切って0の位置より2つ左に進んでみます。
こうしてたどり着くのが -2 という数です。
私たちは負の数を「発見」したのです。
まとめておきましょう。
正の数は、数直線では、0の位置から点を右に動かしたところにあります。負の数は0の位置から点を左に動かしたところにあります。このように、数の正負は、数直線上では、0の位置を起点として右向きと左向きで表すことができます。
数直線と掛け算
足し算と引き算について考えたので、次に掛け算について、数直線を使ったイメージを見ていきます。
例として、2×3=6 という計算について、数直線を使って考えてみます。
まず、点を1の位置に置き、数直線の長さを2倍に伸ばします。
次に、数直線の長さをさらに3倍に伸ばします。
すると、結果として、点はもともとの数直線の6の位置にきます。

これが、2×3=6 という計算の数直線でのイメージです。
足し算と引き算を考えたときには、計算を始める前に0の位置に点を置きました。掛け算の場合は、最初に1の位置に点を置きます。これは、上の図でも分かるとおり、掛け算という計算は、数直線を伸び縮みさせることで表せるためです。出発点が0の位置だと、いくら数直線を伸ばしても0の位置から動かないので、いろいろな数を表すことができなくなります。
では続いて、2×(-3)という計算について考えてみます。
まず、点を1の位置に置き、数直線の長さを2倍に伸ばします。
ここまではいいでしょう。問題になるのは次です。数直線の長さを -3倍にしなければなりません。これはどうすればいいでしょうか? そのヒントは、上で見せた 2×3=6 の計算の図にあります。
上の図では、数直線をまず2倍に伸ばし、次にさらに3倍に伸ばすときに、1の位置に◆印をつけてあります。そして、この◆印は、数直線を3倍に伸ばしたあと、3の位置にくることが分かります。
つまり、数直線を -3倍にするには、1の位置につけた◆印が -3の位置にくるようにすればよいのです。

こうして、結果として、初めにあった点は、もともとの数直線の -6 の位置にきます。
これが、2×(-3)= -6 という計算の数直線でのイメージです。
ここで、上の図で起こっていることを整理してみます。
数直線を -3倍にするときに、1の位置につけた◆印を -3の位置にもっていきました。1 は正の数で右向きの数ですが、-2 は負の数で左向きの数です。つまり、数の向きが逆になったことになります。そして、◆印の位置が逆になったのに伴って、数直線全体の向きが逆になります。
ここで、いよいよ、(-2)×(-3)という計算について考えてみます。
まず、点を1の位置に置き、数直線を -2倍に伸ばします。このとき、数直線の向きが逆になります。
次に、数直線を -3倍に伸ばします。これにより、数直線の向きが再び逆になり、元に戻ります。
すると、結果として、点はもともとの数直線の6の位置にきます。

これが、(-2)×(-3)=6 という計算の数直線でのイメージです。
マイナス記号のルール
ここで、こんなふうに考えてみましょう。
数式の中で マイナスの記号 が現れたら、それには 数の向きを逆にする 作用がある、と考えます。例えば、3は右向きの数なので、-3 は左向きの数です。
これをルールと考えて、これまでの計算をすべて見直してみます。
2+3=5 について。
0の位置に点を置き、右に2動かします。
さらに右に3動かします。
結果として点は5の位置にきます。
5-3=2 について。
0の位置に点を置き、右に5動かします。
マイナスの記号があるので、3の向きを逆にして、左に3動かします。
結果として、点は2の位置にきます。
3-5=-2 について。
0の位置に点を置き、右に3動かします。
マイナスの記号があるので、5の向きを逆にして、左に5動かします。
結果として、点は -2 の位置にきます。
2×3=6 について。
1の位置に点を置き、数直線を2倍に伸ばします。
さらに数直線を3倍に伸ばします。
結果として、点は6の位置にきます。
2×(-3)=-6 について。
1の位置に点を置き、数直線を2倍に伸ばします。
マイナスの記号があるので、数直線の向きを逆にします。
さらに数直線を3倍に伸ばします。
結果として、点は -6 の位置にきます。
(-2)×(-3)=6 について。
1の位置に点を置きます。
マイナスの記号があるので、数直線の向きを逆にします。
数直線を2倍に伸ばします。
マイナスの記号があるので、もう一度、数直線の向きを逆にします。
数直線を3倍に伸ばします。
結果として、点は6の位置にきます。
このように、上のルールを使うと、正負の数の足し算、引き算、掛け算に出てくるマイナスの記号を、すべて、同じように考えることができます。
このルールにもとづくならば、負の数×負の数=正の数 となる理由は、数の向きを2回逆にすると元の向きに戻るからだ、と答えることができます。
では、応用問題です。2-(-3)はどうなるでしょうか?
0の位置に点を置き、右に2動かします。
次は、括弧のなかを先に考えなければいけません。マイナスがあるので、左に3動かす、という意味です。
その前にさらにマイナスがあるので、向きを逆にして、右に3動かします。
結果として、点は5の位置にきます。
負の数×負の数=正の数 の解説では、よく、速度×時間=距離 の関係が使われます。
例えば、東向きに進んでいる車の速度を正の速度とし、西向きに進んでいる車の速度を負の速度とします。このとき、西向きに進んでいる車は、未来には、現在の位置より西側にあります。しかし、過去には、現在の位置より東側にありました。これは簡単に想像がつくでしょう。
この記事ではこれまで、正の向きを赤色で、負の向きを青色で表してきました。上の過去の車の位置の計算は、
西向き × 過去 = 東側
というように、負の向きの数をふたつ掛け算したもので、負の数×負の数=正の数 となっています。この計算は想像通りの結果になっています。
現実の問題は、この車の位置のように単純ではなく、もっともっと複雑で、簡単には結果を想像できなかったりします。この記事で解説した数の向きのルールは簡単なものですが、それでも、複雑な問題を解くときに、ひとつ一つ、マイナスがあるから向きが逆になって、などと考えるのは大変です。
そこで、数の向きのルールをさらに単純なルールにしたものが 負の数×負の数=正の数 というルールなのです。
余談・虚数
ここからは余談になります。中学校の数学の範囲をこえた話をします。
いま、ある数をふたつ掛け算すると4になるとします。このとき、ある数はいくらでしょうか? これは平方根についての問題で、中学3年生で学びます。
2をふたつ掛け算すると4になるので、答えは2、といいたいところですが、それでは満点は取れません。-2もふたつ掛け算すると4になります。満点が取れる答えは 2 と -2 です。
さて、ここで問題です。
ある数をふたつ掛け算すると -1 になりました。このとき、ある数はいくらでしょうか?
この問題を初めて考える人は、まず、-1かな、と思うのではないでしょうか? しかし、-1をふたつ掛け算すると 1 になってしまいます。
(-1)×(-1)=1 について。
1の位置に点を置きます。
マイナスの記号があるので、数直線の向きを逆にします。
マイナスの記号があるので、もう一度、数直線の向きを逆にします。
結果として、点は1の位置にきます。
マイナスの記号には数の向きを逆にする作用があるのでした。向きを逆にする操作を2回行うと、元の向きに戻ってしまいます。
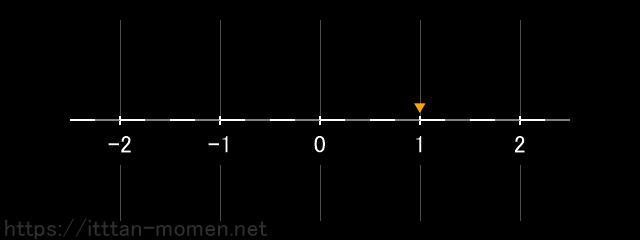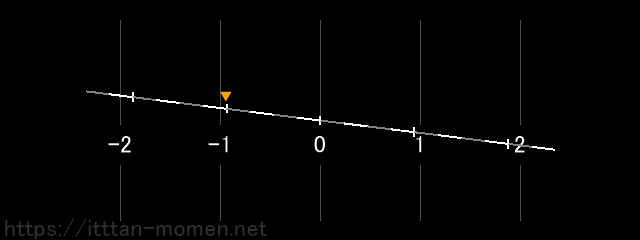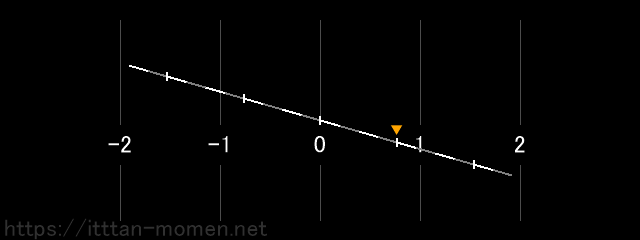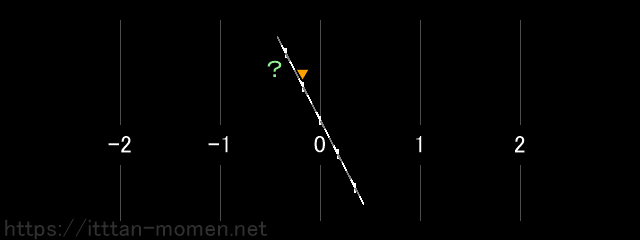
ある操作で数の向きを2回変えると逆向きになる。そのとき、「ある操作」は数の向きをどのように変えるのか? これが、この問題が問うていることです。
そこで、数の向きを逆にしている途中で操作を止めてみたらどうなるでしょうか? そのとき、1の位置に置いた点はどこに移動しているでしょうか?
私たちはこれまで、数を直線上の点で表してきました。しかし、この操作は直線で表すことができません。
そこで、直線の壁を壊して、数の空間を平面に広げます。そして、1の位置に置いた点を 90° 回転させる操作を考えます。こうしてたどり着いた点の表す数を i で表し、虚数単位 と呼びます。
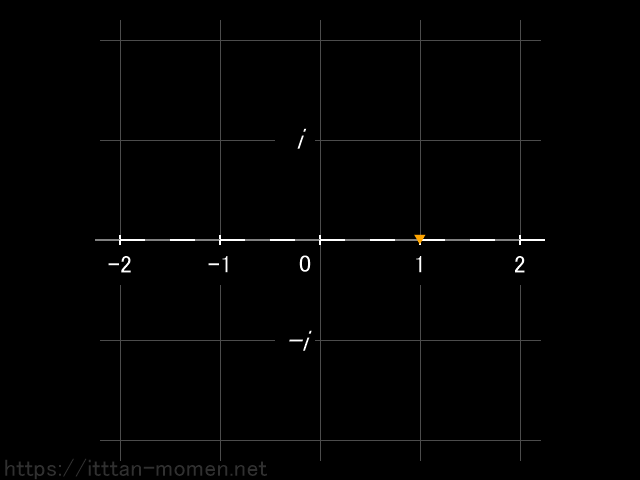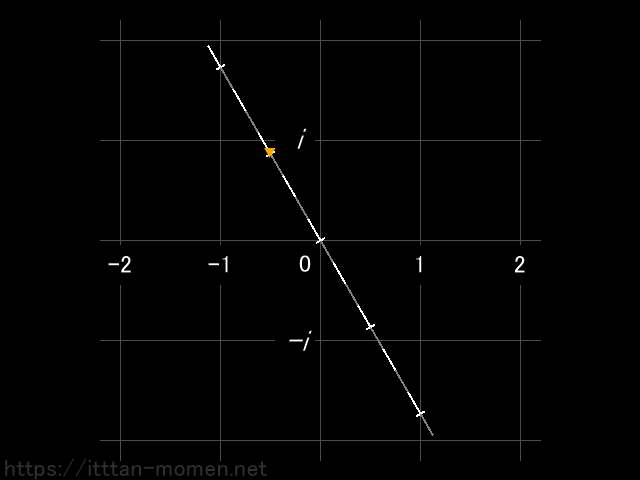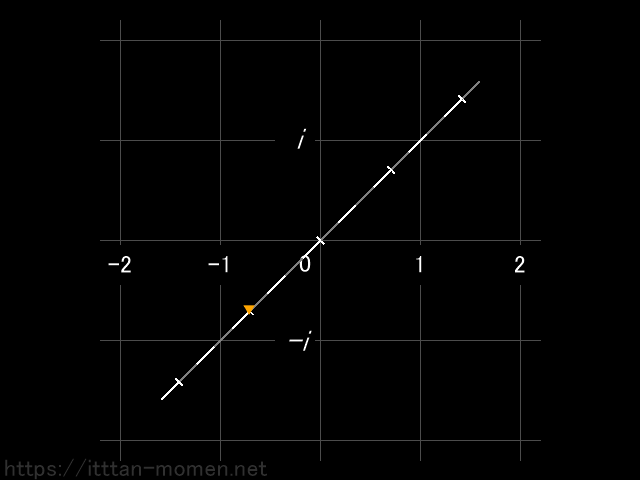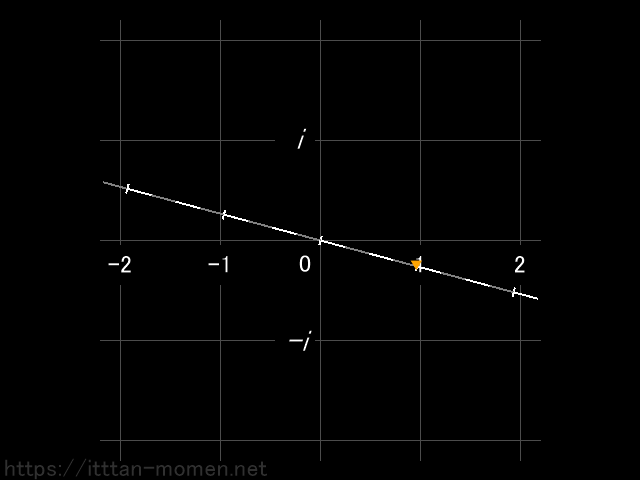
これまで、私たちが馴染んできた数直線上の数は 実数 とよばれます。一方、新しく登場した縦軸上の数は 虚数 とよばれます。こうして広げた数の空間を 複素平面 とよびます。そして、これまでは、数というのは 2 とか -3 とかのひとつの実数で表されていたのですが、複素平面上の数は、ふたつの実数と i を組み合わせて、2-3i というように表されます。2が上の図の左右の位置を表し、-3i が上下の位置を表すのです。このふたつの実数と i で表された数を 複素数 とよびます。
ここで、新しく登場した i について、次のようにルールを決めます。
数式の中で i の記号 が現れたら、それには 数の向きを 90° 回転する 作用がある、と考えます。例えば、3は右向きの数なので、3i は上向きの数です。
いよいよ、問題の答えです。ふたつ掛け算したとき -1になるのは、i という数です。
といいたいところですが、これでは満点は取れません。1の位置に置いた点を 90° 回転させるには、点を上にもっていく経路だけではなく、下にもっていく経路もあるはずです。つまり、逆回転させる経路です。
数の向きを逆にするのはマイナスの記号でした。i の向きの逆、つまり、- i もこの問題の答えです。この問題で満点を取るには、i と – i、と答えなければなりません。
日本の学校では、2次方程式について教える過程で虚数を導入します。2次方程式の解の公式には平方根が含まれています。その平方根の中身が負の数であっても、2次方程式が解をもつようにする、という理由で虚数単位 i が教えられるのです。しかし、多くの人にとって、この説明による i の意味は分かりにくいもののようです。
実際、虚数の「虚」という漢字には、空っぽである、という意味があります。虚数という用語は、実体がない数、といった意味を表すために作られたのでしょう。虚数は英語では imaginary number とよばれます。想像上の数、といった意味になります。
しかし、ある数に i を掛け算していくと 90° ずつ回転していくことからも分かるように、複素数は、回転や振動、波動を表すのに非常に便利な数で、科学の幅広い分野で使われています。
複素数というのは、一定の計算ルールを与えられたふたつの実数の組なのであって、実体のない想像上の数などではありません。
この記事の解説を読めば、数学では 0 と 1、そして、i という数には、ほかの数にはない重要な意味があることが想像できると思います。
これらの数がいちどに現れる数式として有名なものに、Euler の等式があります。
\( e^{i\pi} + 1 = 0 \)
この数式には、さらにふたつの数、\( e \) と \( \pi \) が現れます。このうち \( \pi \) は円周率です。\( e \) は自然対数の底やネイピア数と呼ばれる数です。
虚数の説明のところで、i を掛け算すると数の向きが 90° 回転する、という話をしました。このように、数が円周上を回転することが、上の式に \( \pi \) が現れる理由だ、ということは想像ができると思います。しかし、\( e \) の意味について理解するには、指数関数や微分法の知識が必要になります。
どんな数でも 0乗すると 1 になります。例えば、\( 2^0 = 1 \) です。ですので、\( e^0 = 1 \) です。\( \pi \) は弧度法で測った角度で 180° を表しています。この記事の i の説明の図で 1 を回転させるとき、ほんの少しだけ回転させると、わずかに上向きに動くことが分かります。それが i の向きです。
1を i の向きに 180° 回転させると -1 になる。それに 1 を足すと 0 になる。
大雑把にいうと、これが Euler の等式の意味です。


